WEIBULL function

Returns the Weibull distribution. Use this distribution in reliability analysis, such as calculating a device's mean time to failure.

Important: This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.

For more information about the new function, see WEIBULL.DIST function.

Syntax

WEIBULL(x,alpha,beta,cumulative)

The WEIBULL function syntax has the following arguments:

• X     Required. The value at which to evaluate the function.

• Alpha     Required. A parameter to the distribution.

• Beta     Required. A parameter to the distribution.

• Cumulative     Required. Determines the form of the function.

Remarks

• If x, alpha, or beta is nonnumeric, WEIBULL returns the #VALUE! error value.

• If x < 0, WEIBULL returns the #NUM! error value.

• If alpha ≤ 0 or if beta ≤ 0, WEIBULL returns the #NUM! error value.

• The equation for the Weibull cumulative distribution function is:

  

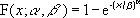
• The equation for the Weibull probability density function is:

  

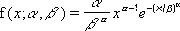
• When alpha = 1, WEIBULL returns the exponential distribution with:

  

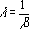
Example

Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.

Data	Description
105	Value at which to evaluate the function
20	Alpha parameter to the distribution
100	Beta parameter to the distribution
Formula	Description (Result)	Result
=WEIBULL(A2,A3,A4,TRUE)	Weibull cumulative distribution function for the terms above (0.929581)	0.929581
=WEIBULL(A2,A3,A4,FALSE)	Weibull probability density function for the terms above (0.035589)	0.035589