Equations for calculating trendlines

Linear

Calculates the least squares fit for a line represented by the following equation:

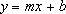
where m is the slope and b is the intercept.

Polynomial

Calculates the least squares fit through points by using the following equation:

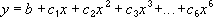
where b and 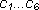are constants.

Logarithmic

Calculates the least squares fit through points by using the following equation:

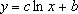
where c and b are constants, and ln is the natural logarithm function.

Exponential

Calculates the least squares fit through points by using the following equation:

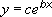
where c and b are constants, and e is the base of the natural logarithm.

Power

Calculates the least squares fit through points by using the following equation:

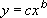
where c and b are constants.

R-squared Value

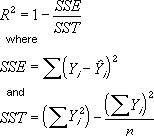
Note: The R-squared value you can display with a trendline is not an adjusted R-squared value. For logarithmic, power, and exponential trendlines, Microsoft Graph uses a transformed regression model.

Moving Average

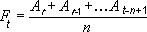
Note: The number of points in a moving average trendline equals the total number of points in the series less the number you specify for the period.