Poisson function

Returns the Poisson distribution. A common application of the Poisson distribution is predicting the number of events over a specific time, such as the number of cars arriving at a toll plaza in 1 minute.

Syntax

POISSON(x,mean,cumulative)

X     is the number of events.

Mean     is the expected numeric value.

Cumulative     is a logical value that determines the form of the probability distribution returned. If cumulative is TRUE, POISSON returns the cumulative Poisson probability that the number of random events occurring will be between zero and x inclusive; if FALSE, it returns the Poisson probability mass function that the number of events occurring will be exactly x.

Remarks

• If x is not an integer, it is truncated.

• If x or mean is nonnumeric, POISSON returns the #VALUE! error value.

• If x ≤ 0, POISSON returns the #NUM! error value.

• If mean ≤ 0, POISSON returns the #NUM! error value.

• POISSON is calculated as follows.

  For cumulative = FALSE:

  

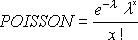
  For cumulative = TRUE:

  

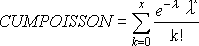
Example

X	Mean	Formula	Description (Result)
2	5	=POISSON([X],[Mean],TRUE)	Cumulative Poisson probability with the specified arguments (0.124652)
2	5	=POISSON([X],[Mean],FALSE)	Poisson probability mass function with the specified arguments (0.084224)