HYPGEOMDIST function

Returns the hypergeometric distribution. HYPGEOMDIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size. Use HYPGEOMDIST for problems with a finite population, where each observation is either a success or a failure, and where each subset of a given size is chosen with equal likelihood.

Syntax

HYPGEOMDIST(sample_s,number_sample,population_s,number_population)

Sample_s     is the number of successes in the sample.

Number_sample     is the size of the sample.

Population_s     is the number of successes in the population.

Number_population     is the population size.

Remarks

• All arguments are truncated to integers.

• If any argument is nonnumeric, HYPGEOMDIST returns the #VALUE! error value.

• If sample_s < 0 or sample_s is greater than the lesser of number_sample or population_s, HYPGEOMDIST returns the #NUM! error value.

• If sample_s is less than the larger of 0 or (number_sample - number_population + population_s), HYPGEOMDIST returns the #NUM! error value.

• If number_sample < 0 or number_sample > number_population, HYPGEOMDIST returns the #NUM! error value.

• If population_s < 0 or population_s > number_population, HYPGEOMDIST returns the #NUM! error value.

• If number_population < 0, HYPGEOMDIST returns the #NUM! error value.

• The equation for the hypergeometric distribution is:

  

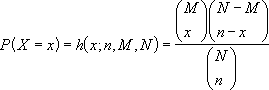
  where:

  x = sample_s

  n = number_sample

  M = population_s

  N = number_population

HYPGEOMDIST is used in sampling without replacement from a finite population.

Example

A sampler of chocolates contains 20 pieces. Eight pieces are caramels, and the remaining 12 are nuts. If a person selects 4 pieces at random, the following function returns the probability that exactly 1 piece is a caramel.

Sample_s	Number_sample	Population_s	Number_Population	Formula	Description (Result)
1	4	8	20	=HYPGEOMDIST([Sample_s],[Number_sample],[Population_s],[Number_Population])	Hypergeometric distribution for sample and population (0.363261)